You and you friend rolled a die 10 times each. Your friend rolls were:
- {1,2,3,4,5,1,2,3,4,5} with average value of 3
and your were:
- {1,2,3,1,2,3,1,2,3,4} with average value of 2.2
Is it fair to say that your friend's die is biased to perform better?
i.e. you are have two hypotheses at hand:
- your dice are equal (the Null Hypothesis)
- his die is better (the Alternative Hypothesis)
The trick is to assume that your dice' distributions are equal and compute the probability that the scenario at hand could happen - i.e his avarage is better.
Since additional collection of samples is not possible you can employ this idea:
Overall combined sample is: {1,2,3,4,5,1,2,3,4,5,1,2,3,1,2,3,1,2,3,4} and, if dice distributions are equal, any 10 of these values could equally likely happen in YOUR dice roll. The mean difference is 3-2.2=0.8, so for each 184756 ways to choose 10 samples out of 20 lets compute how often difference of means is bigger than 0.8.
It happens with probability 0.1 which is 10% - i.e. getting diffence of 0.8 or bigger happens only in 10% of the cases - so it's NOT fair to assume his die is better, because 10% is not too small of a chance - collect more samples.
Here is the distribution for mean difference:
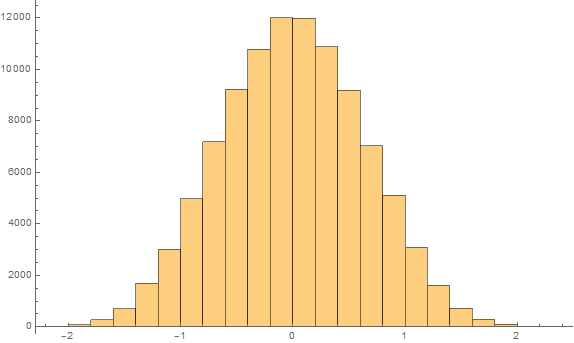
Note that nowhere we made the assumption that the die roll is uniform i.e. numbers 1-6 are equally likely to happen - this makes this method more powerful - it does not depend on any additional assumptions about uniformity or normality of the data at hand.
Here are additional permutational hypothesis testing ideas:
- Equality of means:
- example above
- also look Mann-Whitney rank test
- To test equality of mean to some value Mu:
- assumption is: distribution is symmetric around Mu
- if distribution is symmetric around Mu that means for every value Xi value Xi' reflected around Mu is equally likely
- for example if Mu = 0, then for every "Xi" value "-Xi" is equally likely, compute all 2^n sign changes
- Equality of paired distribution:
- you have X1 and X2 which are paired (example: student exam score before and after 8 hours of sleep)
- you want to compute if there are any changes Xi distributions
- if there distributions are equal then pair X1i and X2i could swap places
- compute probabilities for every 2^n outcomes