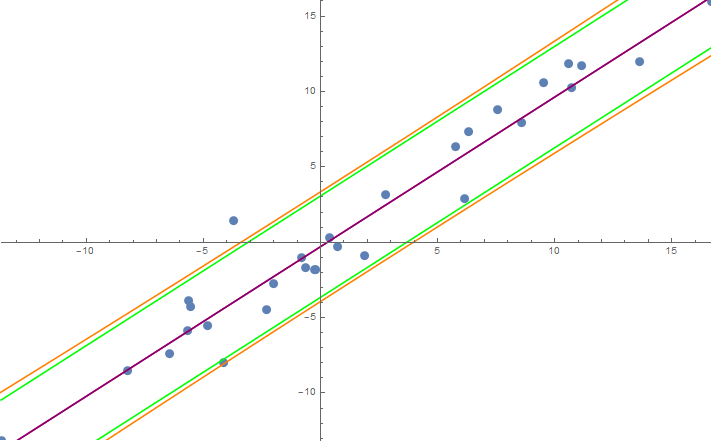
Assume you have created model a(X) to predict values of some sample Yi based on Xi. You can actually predict the confidence intervals for new, never seen Y.
The simplest thing you can do is just calculate the variace of (a(X) - Y) based on the sample you have. That actually will be the maximum likelyhood estimator of the variance. And use normal distribution confidence intervals:
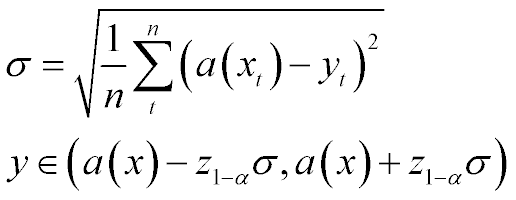
use 1.96 as z(1-alpha) for 95% confidence interval.
But maximum likelyhood estimator overfits the actual model, if your sample size is small and you fitted a simple linear regression with
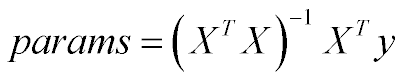
params actually behave like normal variables because they are a linear combination of Y:
- their unbiased estimator of sigma can be calculated
- you can use student T distribution to have unbiased prediction intervals
Given K regressors calculate your interval as follows:
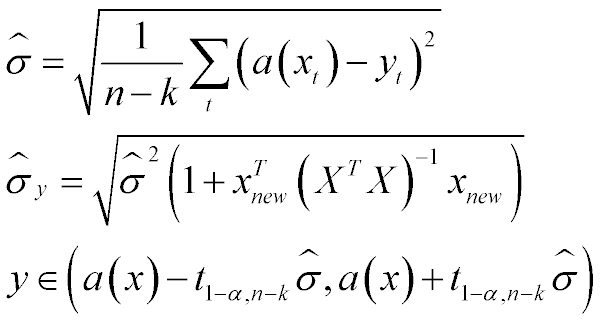
where 't' is the student distribution with n-k degrees of freedom.
The number of regressors K is the number of columns in matrix X and k=2 when you fit a*x+b because b is an additional regressor.